
This is a companion web page for the paper Drawing Equirectangular VR Panoramas with Ruler, Compass, and Protractor, which heavily revises and expands upon preliminary results presented in my Macau conference paper, Drawing Equirectangular Perspectives for Immersive Panoramas.
Currently it holds the VR panoramas mentioned in the text, an equirectangular grid, and a tutorial video.
The colored grid helps you to keep track of lines as they cross the horizon. I use it for both my own handmade sketching and for digital sketching with my drawing program prototype Eq A Sketch 360. It has been used by a lot of artists, and even adopted by Microsoft's app Sketch 360 (which also uses my algorithms for calculating equirectangular lines).
You can view my ongoing series of equirectangular drawing tutorials at my youtube channel to learn how to use the grid.
My plan is to place here, as time permits, more representative examples, notes, and code, to further supplement the paper.
On this website you can also see:
The companion page for my paper on fisheye spherical perspective (Ruler, Compass, and Nail: Constructing a Total Spherical Perspective).
My experimental equirectangular drawing app, Eq A Sketch 360, and a paper about it that I wrote for the Artech 2019 meeting.
Equirectangular spherical perspective isn't as nice as azimuthal equidistant spherical perspective in terms of great circle plots. Great circles plot like elevation=arctan(a.cos(azimuth)), which with the apex at high latitudes makes for some rather squarish lines. But these too can be well approximated by ruler and compass (see my paper above).
The good thing about these equirectangular perspectives is that Flickr, Google, Facebook, and so on, know how to render them as VR panoramas. In short, they wrap the perspective drawing around a sphere and put you at the center. What you get is a spherical anamorphosis, i.e., the immersive optical illusion of being inside the original environment.
In the examples below you can see the flat perspective, drawn by hand, followed by its VR panorama. Click on the panorama and then drag the mouse to navigate it.
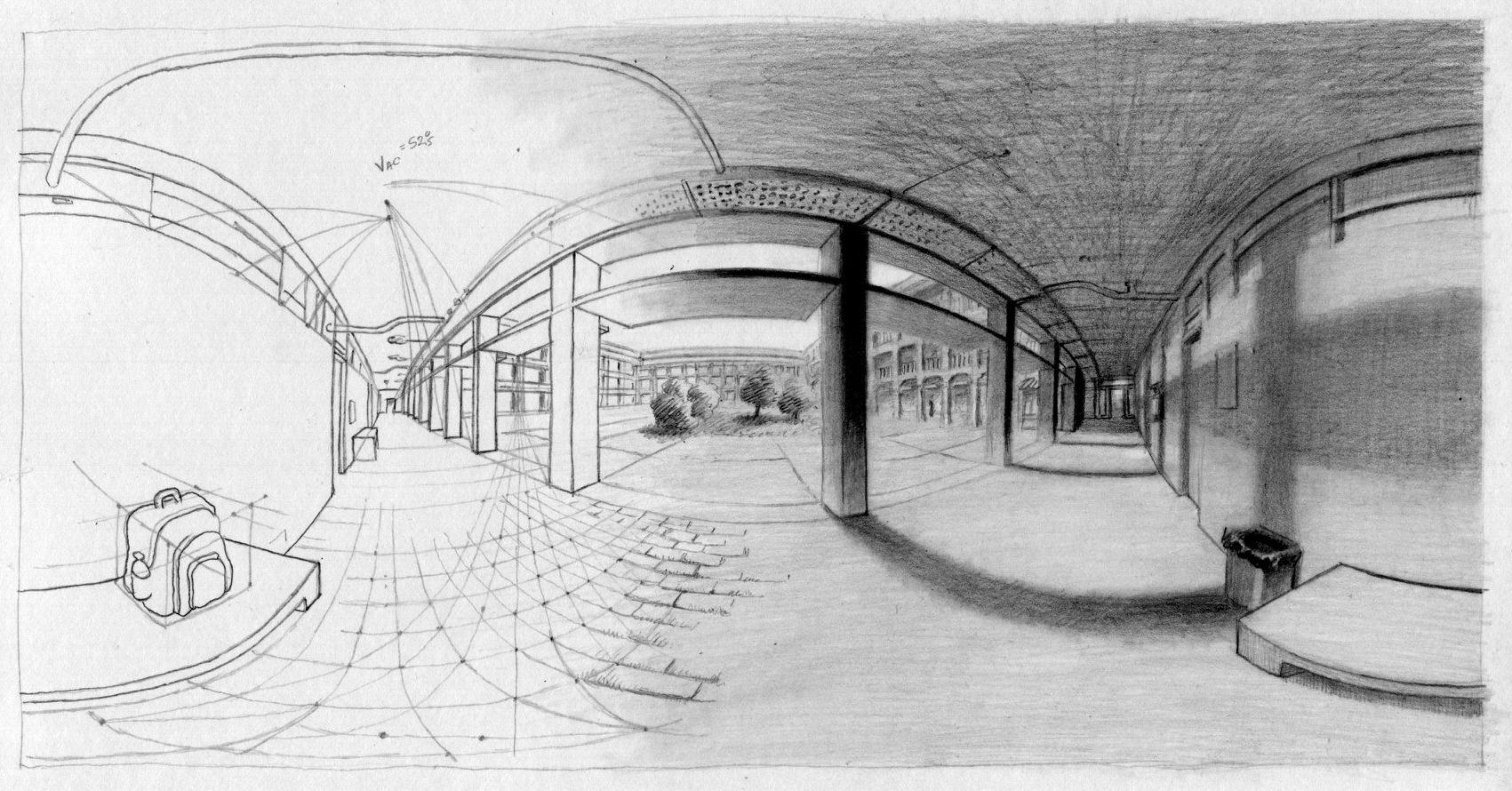
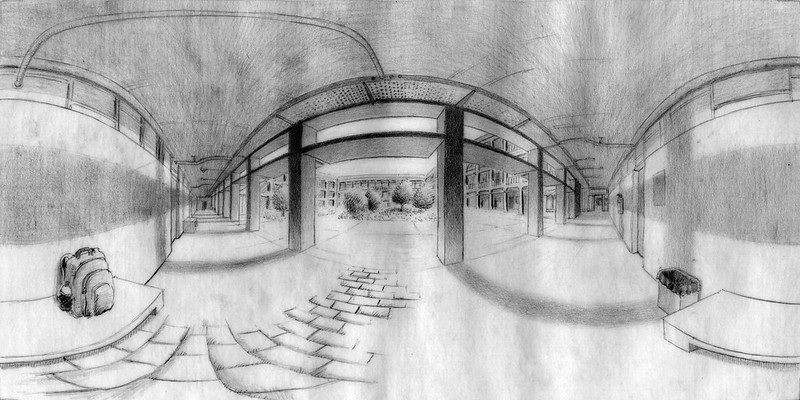
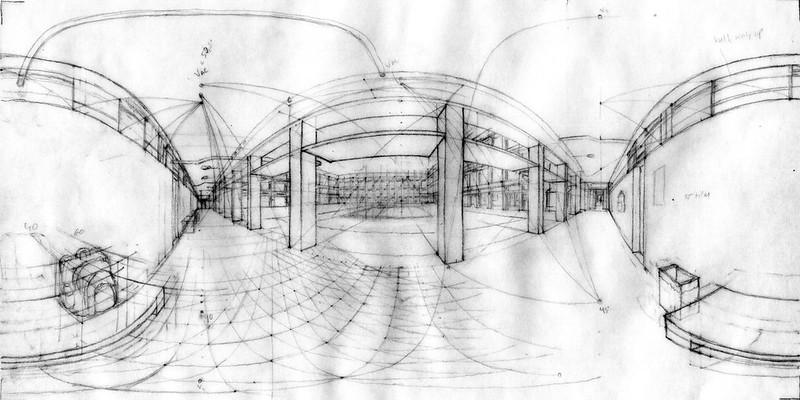
A drawing of ISEL's inner courtyard.
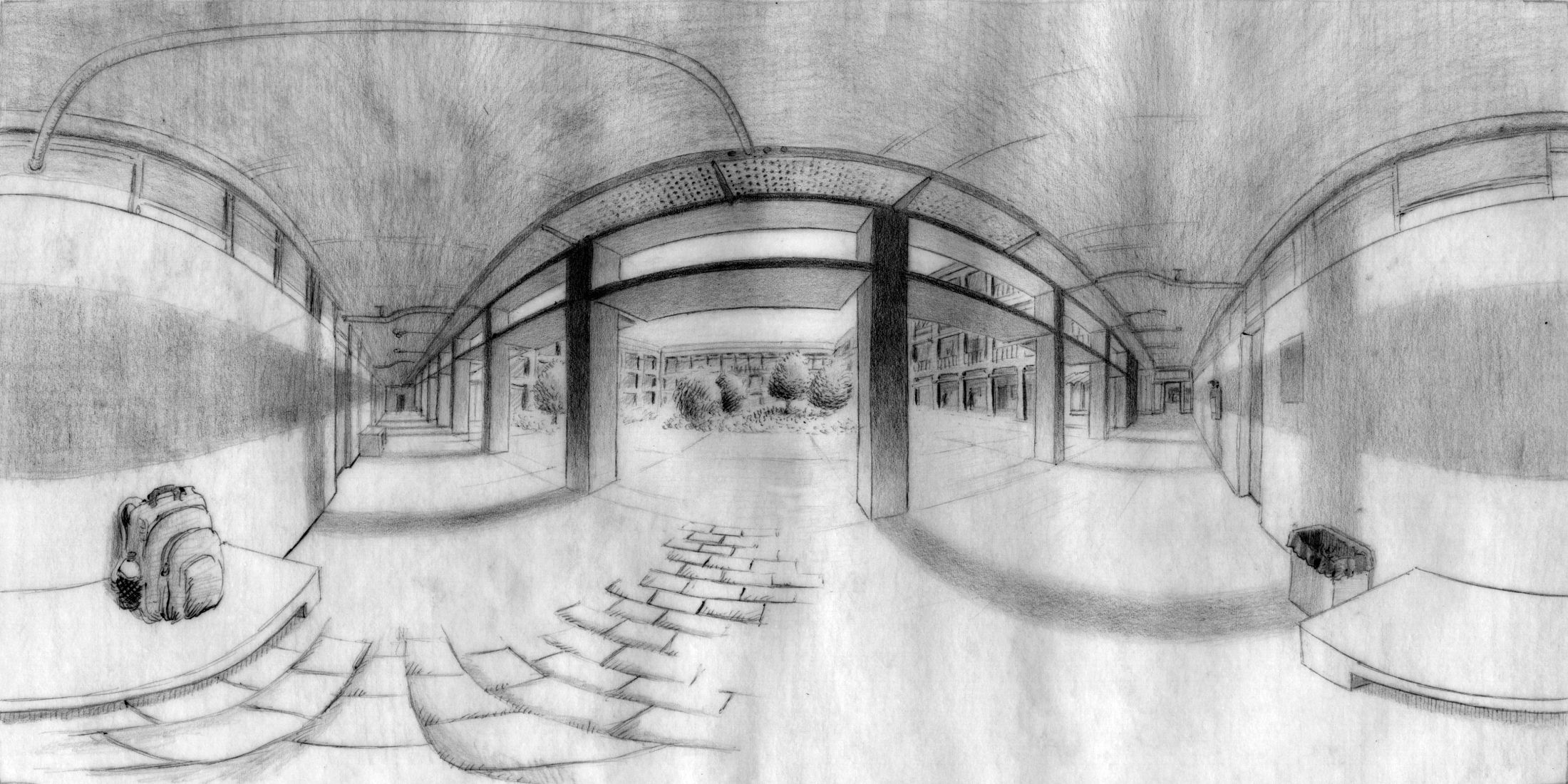
Click on the picture below to see it as a VR panorama.
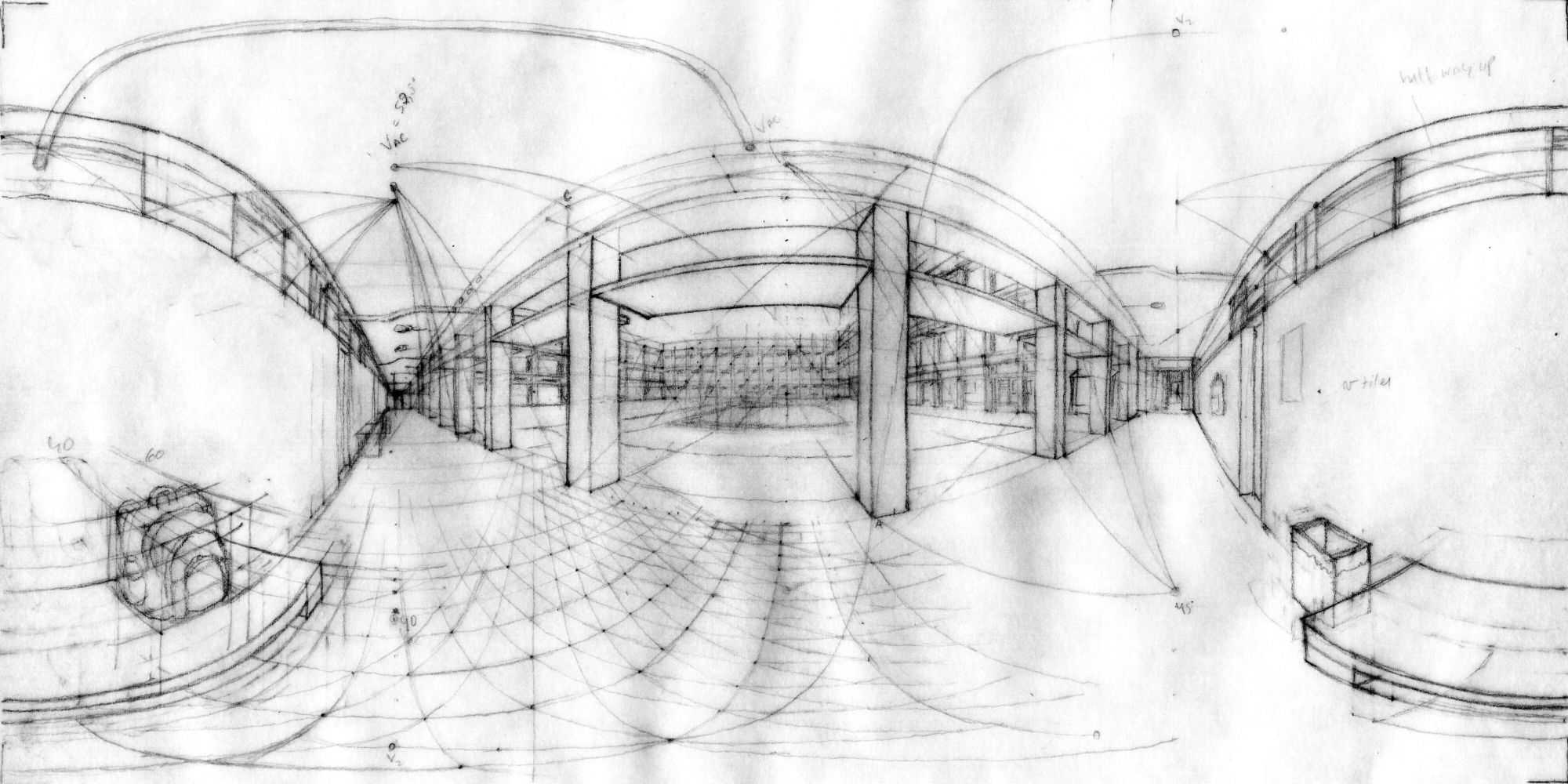
Construction of the vanishing points of ISEL's inner courtyard.
Click on the picture below to see it as a VR panorama.
A cubical room seen from its center.

Click on the picture below to see it as a VR panorama.

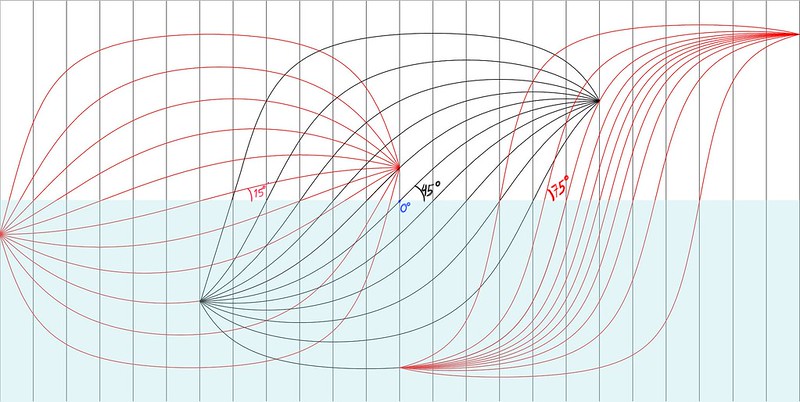
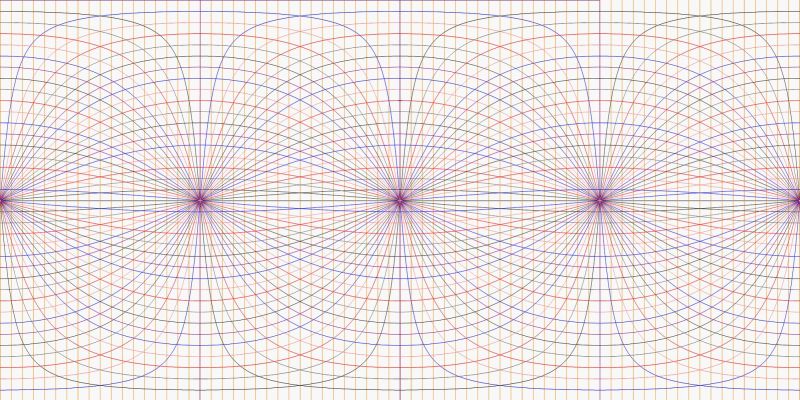
Below we have an equirectangular perspective of three pencils of straight lines, going to 15, 45, and 75 longitude vanishing points respectively, from left to eight. We can see that these lines take a rather complex sigmoidal shape. Yet they can all be obtained by translations and crops from the equirectangular grid below (see my video tutorial on the sliding grid method).

Click on the picture below to see it as a VR panorama.
A drawing from observation of my stairwell.

Click on the picture below to see it as a VR panorama.

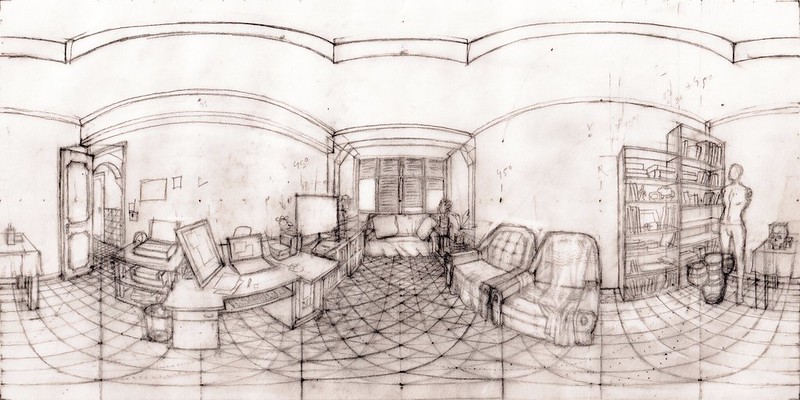
A drawing of a room from observation. Notice the regular tiling on the floor.
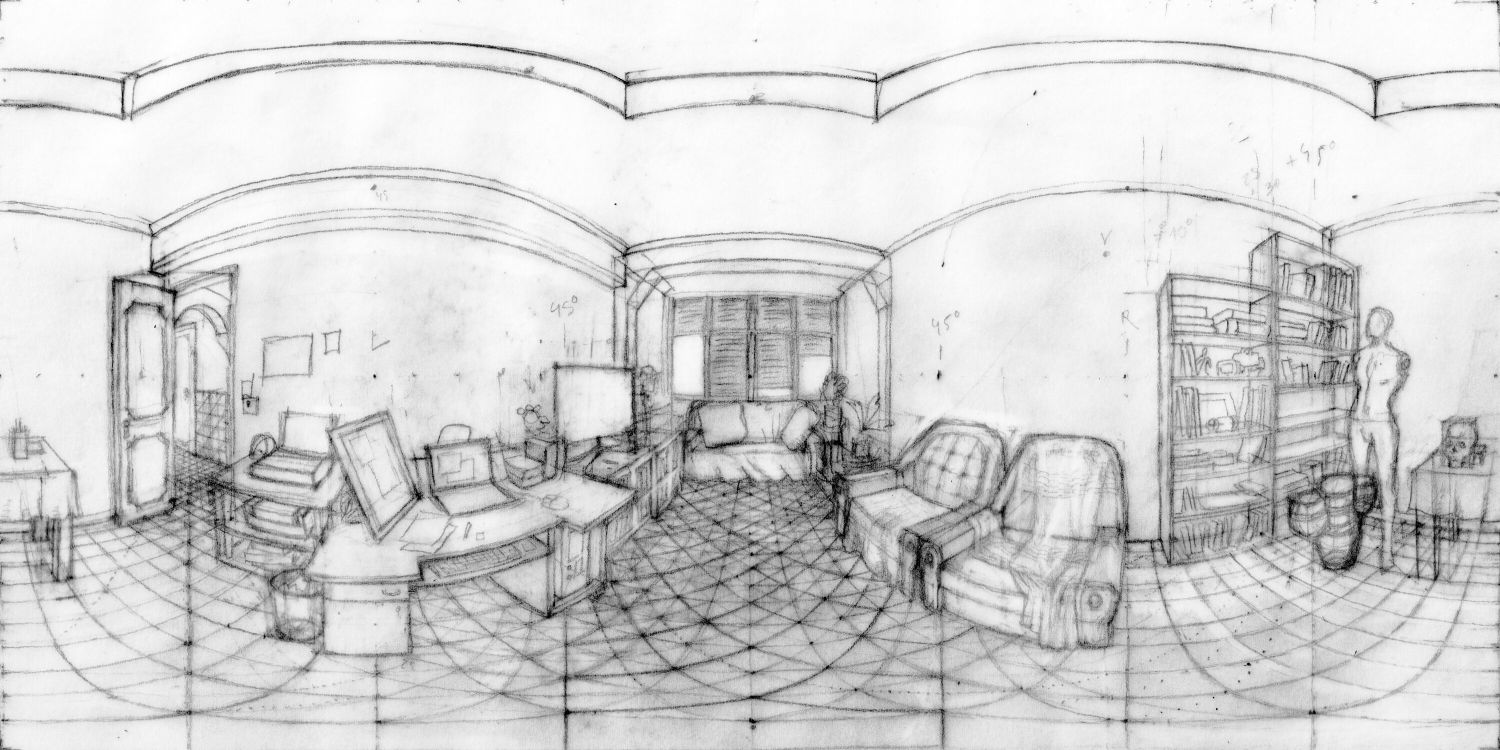
Click on the picture below to see it as a VR panorama.
You can see a video about the sliding grid method which I introduced in my paper, Drawing Equirectangular VR Panoramas with Ruler, Compass, and Protractor.
The following grid may be useful if you want to apply the sliding grid method. You can download it in higher resolution here. You can learn how to use it in my youtube channel.
EXIF injections:
Placing VR panoramas on facebook requires injection of the correct EXIF data. An easy way to do it online is through the Thexifer web app.
You can for instance choose Make as "RICOH" and Model as "RICOH THETA S".
An alternative, quicker way to do it is with The 360 Toolkit, a web site that is also very practical for converting between equirectangular perspective and cubemaps.
An advanced editor for fancier Exif stuff on the desktop is ExifTool, and you can use it with jExifToolGUI as a graphical frontend.